Finite Elemen Method (FEM) atau Metode Elemen Hingga

Metode Finite Elemen atau metode elemen hingga, adalah suatu metode perhitungan faktor keamanan menggunakan bantuan software sehingga  memungkinkan untuk menangani masalah-masalah teknik geoteknik yang rumit termasuk adanya faktor tekanan air pori, teratur maupun tidak dan berbagai bentuk bidang gelincir.

Dalam metoda elemen hingga atau FEM, tidak dilakukan asumsi bidang longsor. Faktor keamanan dicari dengan mencari bidang lemah pada struktur lapisan tanah. Faktor keamanan didapatkan dengan cara mengurangi nilai kohesi, c, dan sudut geser dalam tanah, 𝝓 , secara bertahap hingga tanah mengalami keruntuhan. Nilai faktor keamanan, kemudian dihitung sbb:

dengan; ΣMSF= faktor keamanan; Creduced dan 𝝓reduced = nilai c dan 𝝓 terendah yang didapat pada saat program Plaxis mengatakan tanah mengalami keruntuhan (soil body collapse). Proses perhitungan ini dalam diagram keruntuhan Mohr diilustrasikan pada Gambar dibawah; Dalam program PLAXIS metode ini disebut “Phi-c reduction”. 

Gambar 1 – Proses Perhitungan Faktor Keamanan dalam FEM 

Sebagaimana disebutkan pada pendahulan bahwa analisa kestabilan dengan FEM ini dilakukan dengan menggunakan program Plaxis. Suatu hal yang perlu dikemukakan disini adalah bahwa dalam analisa Undrained untuk tanah berbutir halus terdapat tiga cara (kemungkinan masukan) di dalam PLAXIS, yaitu: 

• Undrained A: Tipe prilaku material dipilih undrained dan parameter-parameter masukan yang dipakai adalah parameter kuar geser efektif (c’,ϕ’, ψ’) dan parameter kekakuan efektif (E’50,ν’). Perhitungan undrained dilakukan dalam analisis tegangan efektif. 
• Undrained B: Tipe perilaku material dipilih undrained dan masukan yang dipakai adalah parameter kuar geser tegangan total (c=cu, ϕ=0, ψ=0) dan parameter kekakuan efektif (E’50,ν’). Perhitungan undrained dilakukan dalam analisis tegangan efektif. 
• Undrained C: Tipe prilaku material dipilih drained dan parameter-parameter yang dipakai sebagai input adalah parameter kuar geser tegangan total (c=cu,ϕ=0, ψ=0) dan kekakuan total (Eu,ν=0,495). Perhitungan undrained dilakukan dalam analisis tegangan total. 

Perhitungan kondisi Undrained, dilakukan dengan menggunakan ke tiga cara di atas. Bila diperlukan perhitungan kondisi drained, maka semua parameter masukan dalam parameter efektif dan tipe material dipilih drained. Model tanah yang dipakai adalah Model Mohr Coulomb.

Untuk model Mohr-Coulomb, ada enam sifat material yang diperlukan. Properti ini adalah sudut geser (φ), kohesi (c), sudut dilatasi (ψ), modulus Young (E), rasio Poisson (ν) dan berat satuan tanah (γ). Modulus Young dan rasio poisson memiliki pengaruh besar pada deformasi dihitung sebelum kegagalan lereng, tetapi memiliki sedikit pengaruh pada faktor keamanan dalam perhitungan analisis stabilitas lereng (Rocscience, 2001). Pelebaran sudut, (ψ) mempengaruhi secara langsung perubahan volume selama tanah menyusut. Jika (ψ=φ), aturan aliran plastisitas dikenal sebagai "berhubungan", dan jika (ψ ≠ φ), aturan aliran plastisitas dianggap sebagai "tidakberhubungan".

Untuk pembahasan lebih lajut serta praktikalnya dapat dibaca pada artikel yang telah saya terjemahkan disini

Read More

Analisis Kestabilan Lereng Tambang Metode Irisan (Method of Slice) atau Metode Fellenius

Metode irisan atau sering juga disebut metode fellenius atau Swedish Circle Method (1936) and May and Brahtz (1936) termasuk kedalam salah satu metode analisis kestabilan lereng dengan analisis Kesetimbangan Batas atau Limit Equilibrium.

Metode Irisan telah menjadi metode yang urnum digunakan dalam menganalisis kestabilan lereng dan timbunan. Metode metode ini menyediakan sarana yang efektif untuk analisis kuantitatif dan semua metode pasti selalu berhubungan dengan masalah statis tak tentu. Penyelesaian angka keamanan membutuhkan pailing sedikit satu asurnsi yang berkenaan dengan gaya-gaya antar irisan (interslice forces). Asumsi yang paling umum dibuat ialah yang berkenaan dengan arah, besar dan titik kerja (point of application) dari gaya-gaya antar irisan.

Metode Fellenius (Ordinary Method of Slice) diperkenalkan pertama kali oleh Fellenius (1927,1936) bahwa gaya memiliki sudut kemiringan paralel dengan dasar irisan faktor keamanan dihitungn dengan keseibangan momen. Fellenius menganggap gaya –gaya yang bekerja pada sisi kanan-kiri dari sembarang irisan mempunyai resultan nol pada arah tegak lurus bidang longsor. Dengan anggapan ini keseimbangan arah vertikal dan gaya-gaya yang bekerja dengan memperhatikan tekanan air pori sebagai berikut:

Faktor aman didefinisikan:

Jika terdapat gaya-gaya lain selain berat tanahnya sendiri, misalnya bangunan di atas lereng, maka momen akibat beban ini diperhitungkan sebagai Md. Metode Fellenius banyak digunakan dalam prakteknya, karena cara hitungan sederhana dan kesalahan hitungan yang dihasilkan masih pada sisi aman.

Untuk praktik perhitungannya dan agar lebih memudahkan, teman teman dapat dilihat pada video dibawah ini; 

  Source : Vedprakash Maralapalle from Swedish Circle Method, , Mumbai University Solved Example.

Read More

Analisis Kestabilan Lereng dengan Metode Elemen Hingga (Finite Elements)

Tulisan ini saya terjemah dan sarikan dari sebuah paper yang di publikasikan oleh D. V. GRIFFITHS dan P. A. LANE. 

sudah cukup lama sebenarnya tangan ini gatel ingin membahas metode finite elemen yang saat ini sangat populer jika dibanding dengan metode tradisional Limit Equilibrium yang pada kesempatan lain akan saya coba buat artikelnya. Ayo coba kita lihat dan resapi sebuah metode yang memiliki kompleksitas tinggi, dan juga saya sambil belajar, let's start

---------------------------------------------------------------------------------------------------------------

Mayoritas analisis kestabilan lereng yang dilakukan saat ini masih menggunakan pendekatan keseimbangan batas tradisional yang melibatkan metode irisan yang pada dasarnya tetap tidak berubah selama beberapa dekade.

Ini bukan hasil yang dibayangkan ketika Whitman & Bailey (1967) menetapkan kriteria untuk metode yang muncul kemudian menjadi mudah diakses oleh semua insinyur.

Metode elemen hingga merupakan pendekatan alternatif yang powerful untuk analisis stabilitas lereng yang akurat, serbaguna dan membutuhkan lebih sedikit asumsi a priori, terutama, mengenai mekanisme failure.

longsoran pada lereng dalam model elemen hingga terjadi "secara alami" melalui zona di mana kekuatan geser tanah tidak cukup untuk menahan tegangan geser.

Paper ini menjelaskan beberapa contoh analisis stabilitas lereng elemen hingga dengan perbandingan terhadap metode solusi lainnya, termasuk pengaruh permukaan bebas terhadap stabilitas lereng dan bendungan.

Output grafis disertakan untuk menggambarkan deformasi dan mekanisme longsor/failure. 

Dikatakan bahwa metode elemen hingga untuk analisis kestabilan lereng adalah alternatif yang lebih kuat dibandingkan dengan metode kesetimbangan batas tradisional dan penggunaannya yang luas sekarang harus menjadi standar dalam praktik geoteknik.

Pendahuluan

Analisis elasto-plastik dari persoalan geoteknik dengan menggunakan metode elemen hingga (FE) telah diterima secara luas pada "arena" penelitian selama bertahun-tahun; namun, penggunaan rutin secara aktualnya dalam praktik geoteknik untuk analisis stabilitas lereng masih terbatas.

Alasan dari kurangnya penerimaan ini tidak sepenuhnya jelas; Namun, para ahli yang menajurkan teknik FE pada sisi akademis harus mengambil tanggung jawab.

Para insinyur dilapangan sering kali skeptis akan perlunya kompleksitas seperti itu, terutama mengingat buruknya kualitas data properti tanah yang seringkali tersedia dari investigasi rutin. Meskipun keragu-raguan ini ada benarnya, namun ada beberapa jenis masalah geoteknik yang dapat menggunakan pendekatan Elemen Hingga dan memberikan manfaat yang nyata.

Tantangan bagi insinyur berpengalaman adalah untuk mengetahui masalah apa yang akan mendapat manfaat dari penggunaan metode Elemen Hingga dan yang mana yang tidak.

Secara umum, masalah linier seperti prediksi dari proses settlement dan deformasi, perhitungan jumlah aliran akibat rembesan dengan debit tetap atau juga studi efek transien karena proses konsolidasi semuanya sangat dapat diterima untuk solusi yang ditawarkan oleh metode elemen hingga.

Pendekatan tradisional yang melibatkan bagan, tabel atau metode grafis akan sering memadai untuk masalah rutin sehari hari, tetapi pendekatan elemen hingga mungkin dapat menjadi salah satu opsi jika geometri atau variasi material ditemukan yang tidak tercakup oleh solusi grafik tradisional (Limit Equilibrium).

Penggunaan analisis nonlinier dalam praktik geoteknik sehari hari sulit untuk dibenarkan, karena biasanya ada peningkatan yang signifikan dalam kompleksitas yang lebih mungkin membutuhkan bantuan spesialis pemodelan.

Analisis nonlinier secara inheren bersifat iteratif, karena sifat material dan / atau geometri masalahnya sendiri merupakan fungsi dari `solusi '. Keberatan terhadap analisis nonlinear dengan alasan bahwa mereka memerlukan daya komputasi yang berlebihan, bagaimanapun, sebagian besar telah dikalahkan oleh perkembangan dalam, dan penurunan biaya, perangkat keras komputer.

Komputer desktop dengan prosesor standar sekarang mampu melakukan analisis nonlinier seperti yang dijelaskan dalam makalah ini dalam rentang waktu yang wajar hitungan menit tetapi tidak sampai berjam- jam atau hari.

analisis kestabilan dinding lereng menggunakan pendekatan Elemen Hingga nonlinier menawarkan manfaat nyata dibanding dengan metode yang biasa digunakan. Seperti yang akan dibahas pada makalah ini, analisis stabilitas lereng oleh elemen elastoplastic finite adalah akurat, kuat dan cukup sederhana untuk penggunaan rutin sehari hari oleh para insinyur yang melakukannya.

Persepsi tentang metode Finite Elemen / Elemen Hingga sebagai metode yang kompleks dan berpotensi menyesatkan tidak beralasan dan mengabaikan kemungkinan bahwa hasil menyesatkan bahkan juga dapat diperoleh dengan pendekatan "slip circle" konvensional.

Kemampuan grafis dari program FE juga memungkinkan pemahaman yang lebih baik tentang mekanisme longsoran /failure, menyederhanakan output dan menampilkan grafik yang dapat dikelola seperti grafik displacement.

Metode Tradisional Analisis Kestabilan Lereng

Sebagian besar buku pelajaran tentang mekanika tanah atau teknik geoteknik akan menyertakan referensi ke beberapa metode alternatif analisis stabilitas lereng. Dalam sebuah survei metode kesetimbangan batas (Limit Equilibrium) untuk analisis stabilitas lereng yang dilakukan oleh Duncan (1996), karakteristik sejumlah besar metode analisis yang populer adalah termasuk; 

1. Ordinary method of slices (Fellenius, 1936) /metode irisan biasa (Fellenius, 1936),

2. Bishop's Modified Method (Bishop, 1955), 

3. Force Equilibrium methods (e.g. Lowe & Kara®ath, 1960)

4. Janbu's generalized procedure of slices (Janbu, 1968)

5. Morgenstern and Price's method (Morgenstern & Price, 1965) and,

6. Spencer's method (Spencer, 1967).

Meskipun tampaknya ada beberapa konsensus bahwa metode Spencer adalah salah satu metode yang paling dapat diandalkan, buku teks terus menggambarkan metode lain dalam beberapa detail, dan berbagai pilihan metode lain yang tersedia akan membingungkan bagi calon pengguna. Sebagai contoh, kontroversi baru-baru ini ditinjau kembali oleh Lambe & Silva (1995), yang menyatakan bahwa metode irisan yang biasa memiliki reputasi yang buruk. 

Kesulitan dengan semua metode keseimbangan adalah bahwa seluruh analisis didasarkan pada asumsi bahwa massa tanah yang akan longsor dapat dibagi menjadi beberapa irisan. Hal ini yang pada akhirnya akan memerlukan asumsi lebih lanjut yang berkaitan dengan arah gaya samping antara irisan, dengan implikasi yang konsekuen untuk keseimbangan. Asumsi yang dibuat tentang kekuatan-kekuatan / gaya samping adalah salah satu karakteristik utama yang membedakan metode keseimbangan batas (Limit Equilibrium) yang satu dengan yang lain, namun itu sendiri merupakan perbedaan yang sepenuhnya dibuat.

METODE ELEMEN HINGGA UNTUK ANALISA KESTABILAN LERENG

Ulasan Duncan tentang analisis FE lereng terkonsentrasi terutama pada deformasi daripada analisis stabilitas lereng; Namun, perhatian ditarik ke beberapa makalah awal yang penting di mana model tanah elasto-plastik digunakan untuk menilai kestabilan lereng. Smith & Hobbs (1974) melaporkan hasil lereng dengan ϕu = 0 dan memperoleh hubungan yang masuk akal dengan grafik Taylor (1937). Zienkiewicz et al. (1975) mempertimbangkan ϕ', c' lereng dan memperoleh relasi yang baik dengan solusi "slip circle".

Griffiths (1980) memperluas karya ini untuk menunjukkan hasil analis kestabilan lereng yang dapat diandalkan pada berbagai sifat dan geometri tanah dibandingkan dengan grafik Bishop & Morgenstern (1960). Penggunaan metode FE selanjutnya dalam analisis stabilitas lereng telah menambah kepercayaan lebih lanjut pada metode tersebut (mis. Griffiths, 1989; Potts et al., 1990; Matsui & San, 1992). Duncan menyebutkan potensi untuk peningkatkan dari hasil grafis dan pelaporan menggunakan metode elemen hingga FE, tetapi memperingatkan bahwa terhadap akurasi tetap tergantung pada parameter input yang secara tidak langsung sangat bervariasi.

Wong (1984) memberikan ringkasan yang berguna tentang potensi sumber kesalahan dalam pemodelan elemen hingga dalam analisa kestabilan lereng, meskipun hasil terbaru, termasuk yang disajikan dalam makalah ini, menunjukkan bahwa akurasi yang lebih baik sekarang sangat dimungkinkan.

Keuntungan dari Metode Analisis Elemen Hingga

Keuntungan dari pendekatan elemen hingga (FE) untuk analisis kestabilan lereng dibandingkan metode kesetimbangan batas (LE) tradisional dapat diringkas sebagai berikut:

(a) Tidak ada asumsi yang perlu dibuat sebelumnya tentang bentuk atau lokasi permukaan longsor (Failure). Failure terjadi 'secara alami' melalui zona-zona dalam massa tanah di mana kekuatan geser tanah tidak mampu menopang tegangan geser yang diterapkan.

(b) Karena tidak ada konsep irisan dalam pendekatan FE, tidak perlu asumsi tentang kekuatan sisi irisan. Metode FE mempertahankan keseimbangan global sampai "Longsor"/ "Failure" tercapai.

(c) Jika data kompresibilitas tanah yang realistis tersedia, solusi FE akan memberikan informasi tentang deformasi pada tingkat gaya tekanan yang bekerja.

(d) Metode FE mampu memantau longosran progresif dan termasuk kegagalan geser keseluruhan / overall shear failure.

DESKRIPSI SINGKAT TENTANG ANALISIS MODEL ELEMEN HINGGA

Program yang digunakan dalam makalah ini didasarkan erat pada Program 6.2 yang digunakan juga pada paper yang dipublikasikan oleh Smith & GrifFIths (1998), perbedaan utama adalah kemampuan untuk memodelkan geometri yang lebih umum dan variasi properti tanah, termasuk variabel permukaan air dan tekanan air pori.

Kemampuan output grafis lebih lanjut telah ditambahkan. Program ini untuk analisis regangan bidang dua dimensi dari tanah plastis, elastis-sempurna dengan kriteria longsoran Mohr-Coulomb yang memanfaatkan elemen segi empat delapan-simpul (eight node) dengan integrasi berkurang /reduced integration (empat titik Gauss per elemen) dalam penurunan beban gravitasi, penurunan matriks kekakuan dan fase redistribusi tekanan dari algoritma.

Tanah awalnya dianggap elastis dan model menghasilkan tegangan normal dan geser pada semua titik Gauss dalam jala / mesh. Tekanan ini kemudian dibandingkan dengan kriteria failure Mohr-Coulomb. Jika tekanan pada titik Gauss tertentu terletak dalam afilure envelope Mohr-Coulomb, maka lokasi tersebut diasumsikan tetap elastis.

Jika tekanan terletak pada atau di luar amplop kegagalan/ failure envelope, maka lokasi itu dianggap akan melentur. Tegangan hasil dari lenturan ini akan didistribusikan kembali di seluruh mesh menggunakan algoritma visco-plastik (Perzyna, 1966; Zienkiewicz & Cormeau, 1974). Longsoran geser keseluruhan akan terjadi ketika sejumlah titik Gauss yang cukup telah dihasilkan untuk memungkinkan suatu mekanisme failure berkembang.

Analisis yang disajikan dalam makalah ini tidak mencoba memodelkan Tension Crack. Meskipun kriteria `nontension 'dapat dimasukkan ke dalam analisis FE elastoplastik (misalnya Naylor & Pande, 1981), kendala tambahan ini pada tingkat tekanan ini mempersulit algoritma, dan, di samping itu, masih ada beberapa perdebatan mengenai bagaimana "Tension" seharusnya dilakukan dengan benar dan didefinisikan. Diperlukan penelitian lebih lanjut dalam bidang ini.

MODEL TANAH

Model tanah pada analisis ini terdiri dari 6 parameter sebagaimana ditampilkan pada Tabel 1.

Pelebaran sudut (ψ) mempengaruhi perubahan volume tanah selama proses yielding (melentur (?)). Diketahui bahwa perubahan volume aktual yang ditunjukkan oleh tanah selama proses yielding (melentur(?)) cukup bervariasi. Sebagai contoh, material padat-sedang selama proses geser mungkin awalnya menunjukkan beberapa penurunan volume (ψ < 0),  diikuti oleh fase dilatif / pelebaran (ψ > 0), yang akhirnya menghasilkan di bawah kondisi volume konstan (ψ = 0). Jelas, jenis pemodelan volumetrik terperinci ini berada di luar ruang lingkup model plastik elastis-sempurna yang digunakan dalam penelitian ini, di mana sudut pelebaran konstan tersirat.

Pertanyaan kemudian muncul adalah, nilai (ψ) seperti apa yang digunakan Jika ψ = ϕ, maka aturan aliran plastisitas dikaitkan dan perbandingan langsung dengan teorema dari plastisitas klasik dapat dibuat. Ini juga merupakan kasus ketika aturan aliran dikaitkan, karakteristik tegangan dan kecepatan bertepatan, sehingga keputusan yang lebih dekat dapat diharapkan antara mekanisme failure yang diprediksi oleh elemen hingga (FE) dan critical failure surface yang dihasilkan oleh metode kesetimbangan batas (LE).

Terlepas dari potensi keuntungan menggunakan associated flow rule, juga diketahui bahwa aturan aliran terkait dengan model tanah gesekan memprediksi pelebaran yang jauh lebih besar daripada yang pernah diamati dalam kenyataan. Ini pada gilirannya menyebabkan peningkatan prediksi beban failure, terutama dalam masalah `terbatas 'seperti daya dukung (Griffiths, 1982).

Kekurangan ini telah menyebabkan beberapa model tanah konstitutif yang paling sukses untuk menggabungkan plastisitas yang tidak terkait (mis. Molenkamp, ​​1981; Hicks & Boughrarou, 1998).

Analisis stabilitas lereng secara umum relatif tidak terbatas, sehingga pilihan sudut pelebaran kurang penting. Karena tujuan utama dari penelitian ini adalah prediksi akurat dari faktor keselamatan (Fos) dari lereng, nilai kompromi ψ = 0, sesuai dengan aturan non associated flow rule dengan perubahan volume nol selama proses yielding (melentur), telah digunakan di seluruh makalah ini.

Akan ditunjukkan bahwa nilai ψ ini memungkinkan model untuk memberikan faktor keamanan yang dapat diandalkan dan indikasi yang wajar dari lokasi dan bentuk dari potensi bidang failure.

Parameter ϕ', c' merujuk pada kohesi dan sudut gesekan tanah efektif. Meskipun sejumlah kriteria longsoran telah disarankan untuk melakukan pemodelan kekuatan tanah (mis. Griffiths, 1990), kriteria Mohr-Coulomb tetap yang paling banyak digunakan dalam praktik geoteknik dan telah digunakan di seluruh makalah ini. Dalam hal tekanan utama dan dengan asumsi kompresi-konvensi tanda negatif, kriteria tersebut dapat ditulis sebagai berikut:

dimana σ1' dan σ3' adalah tegangan major dan minor dari tegangan efektif, Fungsi (1) failure F dapat diinterpretasikan sebagai berikut;

F<0 maka tegangan terjadi didalam failure envelope (elastis)

F=0 maka tegangan terjadi pada failure envelope (yielding)

F>0 maka tegangan terjadi diluar failure envelope (yielding dan harus didistribusikan ulang).

Parameter elastis E' dan ν' merujuk pada modulus Young dan Poissons Ratio terhadap tanah. Jika nilai Poissons  Ratio diasumsikan (tipikal nilai kering terletak pada kisaran 0.2 < ν' < 0.3), nilai modulus Young dapat dikaitkan dengan kompresibilitas tanah yang diukur dalam oedometer satu dimensi (misalnya Lambe & Whitman, 1969):

Dimana mv adalah nilai koefisien dari nilai kompresi volume / volume compressibility. 

Meskipun nilai aktual yang diberikan parameter elastis memiliki pengaruh mendalam pada deformasi yang dihitung sebelum failure, tetapi nilai tersebut memiliki pengaruh kecil terhadap perhitungan dari prediksi faktor keselamatan dalam analisis kestabilan lereng. Dengan demikian, tanpa adanya data untuk nilai E' dan ν', nilai untuk parameter tersebut dapat diberi nilai nominal (E' = 10^5 kN/m2 dan ν' = 0.3).

Singkatnya, parameter yang paling penting dalam analisis stabilitas lereng menggunakan metode Elemen Hingga secara garis besar adalah sama dengan yang akan digunakan dalam pendekatan tradisional, yaitu, total unit weight (γ), the shear strength parameters ϕ', c', dan geometri dari lereng yang akan dianalisis.

GRAVITY LOADING

gaya yang dihasilkan oleh berat tanah dapat dihitung menggunakan prosedur standar gravitasi "trun-on" yang melibatkan integral pada setiap bentuk elemen :

di mana nilai N adalah fungsi dari bentuk elemen dan superscript e merujuk ke nomor elemen. Integral ini mengevaluasi luas masing-masing elemen, dikalikan dengan berat unit total tanah dan mendistribusikan gaya vertikal secara konsisten ke semua node / simpul.

Gaya elemen ini dirakit menjadi vektor gaya gravitasi global yang diterapkan pada mesh Finite Elemen untuk menghasilkan keadaan tegangan awal.

Dalam perbandingan hasil dalam paper ini dengan solusi kesetimbangan batas (LE) yang umumnya tidak memperhitungkan loading sequence, berdasarkan dari pengalaman telah menunjukkan bahwa faktor keamanan yang diprediksi tidak telalu terpengaruh terhadap bentuk aplikasi gravitasi saat menggunakan model Mohr-Coulomb yang elastis-plastik sempurna. Contoh tidak berpengaruhnya ini akan ditunjukkan kemudian dalam makalah ini.

Faktor keselamatan mungkin bisa saja sensitif terhadap loading sequence ketika menerapkan  complex constitutive laws, seperti percobaan yang dilakukan untuk membuat perubahan volumetrik secara akurat pada lingkungan tidak terdrainasi atau hanya dikeringkan sebagian (partially drain). Sebagai contoh, Hicks & Wong (1988) menunjukkan bahwa jalur tegangan efektif / effective stress path dapat memiliki pengaruh besar pada faktor keamanan lereng yang tidak terdrainase. 

PENENTUAN FAKTOR KEAMANAN

Faktor keselamatan atau factor of safety (FoS) dari lereng tanah didefinisikan sebagai nilai dari parameter kuat geser yang harus dibagi hingga pada lereng tersebut sampai pada titik dimana terjadi failure.(Definisi faktor keselamatan ini persis sama dengan yang digunakan dalam metode kesetimbangan batas tradisional, yaitu ratio of restoring to driving moments). Parameter kekuatan geser difaktorkan sebagai berikut ϕ'f, c'f: 

Metode ini disebut sebagai teknik reduksi kekuatan geser (shear strength reduction technique)(Matsui & San, 1992) dan memungkinkan pilihan yang menarik untuk menerapkan berbagai faktor keselamatan pada ketentuan c' dan tan ϕ'. Namun dalam makalah ini, faktor yang sama selalu diterapkan untuk kedua istilah. Untuk menemukan nilai FOS yang benar, perlu untuk memulai pencarian sistematis untuk nilai FOS yang akan menyebabkan lereng longsor. Ini dicapai dengan program analisis berulang-ulang yang menggunakan urutan nilai FOS yang ditentukan pengguna.

Definisi Failure

Ada beberapa definisi dari bagaimana longsoran / failure mungkin terjadi, seperti some test of bulging of the slope profile (Snitbhan & Chen, 1976), limiting of the shear stresses on the potential failure surface (Duncan & Dunlop, 1969) atau non-convergence of the solution (Zienkiewicz & Taylor, 1989). Ini dibahas dalam Abramson et al. (1995) dari makalah aslinya oleh Wong (1984) tetapi tanpa resolusi. Dalam contoh yang dipelajari pada paper ini, opsi non-konvergensi diambil sebagai indikator failure yang sesuai.

Ketika algoritma tidak dapat bertemu dalam jumlah maksimum yang ditentukan pengguna, implikasinya adalah bahwa tidak ada distribusi tegangan dapat ditemukan yang secara bersamaan dapat memenuhi kriteria kegagalan Mohr-Coulomb dan keseimbangan global.

Jika algoritma tidak dapat memenuhi kriteria ini, maka failure dapat dikatakan telah terjadi. Failure pada lereng dan non-konvergensi numerik terjadi secara bersamaan, dan disertai dengan peningkatan dramatis dalam perpindahan simpul/node  dalam mesh.

sebagian besar hasil yang dipaparkan pada paper ini menggunakan batas sekitar 1000 iterasi dan ditampilkan pada plot grafik FoS dibandingkan dengan  E'δmax/γH^2 

(perpindahan tanpa dimensi), dimana δmax  adalah perpindahan maksimal simpul /nodal pada konvergensi dan H adalah ketinggian lereng. Grafik ini dapat digunakan bersamaan dengan mesh dan perpindahan gaya vektor untuk mengindikasikan faktor keselamatan dan sifat dari mekanisme failure / longsoran.

CONTOH DAN VALIDASI STABILITAS LERENG

Beberapa contoh analisis stabilitas lereng menggunakan metode Finite Elemen sekarang disajikan dengan validasi terhadap analisis kestabilan versi traditional jika memungkinkan. Pertimbangan awal
akan diberikan ke lereng yang tidak mengandung tekanan pori di mana tekanan total dan efektif
adalah sama. Ini diikuti dengan contoh yang tidak homogen lereng tanah liat yang tidak dikeringkan. Akhirnya terendam dan lereng yang sebagian terendam dipertimbangkan tekanan pori mana yang diperhitungkan.

Kasus : Lereng homogen tanpa perlapisan D= 1

Lereng homogen pada gambar 1, memiliki sifat sebagai berikut;

 

Kemiringan lereng terbentuk pada sudut 26,5 derajat dengan perbandingan 2 :1 pada bidang horizontal, dan kondisi batas diberikan sebagai batas vertical pada bagian kiri dan kondisi tetap pada bagian dasar. Beban gravitasi diberikan pada mesh dan percobaan nilai keamanan ditingkatkan secara bertahap sampai akhirnya konvergensi tidak tercapai pada batas iterasi sebagaimana di tampilkan pada tabel 2.

Tabel berikut mengindikasikan 6 percobaan faktor keamanan dengan rentang dari 0.8  hingga 1.4. Pada stiap faktor keamanan merepresentasikan analisis yang independent dimana kekuatan  parameter tanah dengan faktor kemanan pada perhitungan (4) dan (5).

Kolom iterasi mengindikasikan banyakanya nilai iterasi pada tiap nilai faktor keamanan. Algoritma harus bekerja lebih keras untuk mencapai konvergensi dari pendekatan nilai faktor kemanan

Ketika nilai faktor keamanan mencapai 1.4, terjadi peningkatan secara tiba2 pada nilai dimensionless displacement E'δmax/γH^2 , dan algoritma tidak mendapat nilai konvergensi pada batas iterasi. Gambar 2 menunjukkan data dari tabel 2 serta mengindikasikan hasil yang hampir sama antara metode Finite Element atau kesetimbangan batas dengan nilai faktor keamanan pada kasus yang sama menggunakan grafik Bishop & Morgenstern (1960).

Gambar 3 menunjukkan pengaruh ukuran kenaikan beban gravitasi terhadap perpindahan pada contoh 1. Dengan faktor keamanan longsoran pada 1.4 yang diterapkan pada properti tanah, keempat grafik tersebut berhubungan dengan perpindahan maksimum yang diperoleh ketika nilai gravitasi diterapkan pada kenaikan tunggal dibanding dengan kenaikan secara 2, 3, atau 5 kali lipat pada kenaikan yang sama. Gambar juga menunjukkan perpindahan diperoleh dengan beban gravitasi sepenuhnya dipengaruhi oleh kenaikan beban.   

Gambar 4a dan 4b memberikan perpindahan node vector dan deformasi mesh yang berhubungan  dengan ketidak konvergensian dengan faktor keamanan 1.4. Mesh yang terdeformasi berhubugnan dengan solusi ketidak convergensian yang mengindikasikan mekanisme failure. Hal ini disebabkan mesh FE yang relatif kasar, yang harus tetap kontinu bahkan pada kondisi `Longsor '. Analisis FE konvensional tidak dapat memodelkan diskontinuitas kotor di sepanjang permukaan potensi kegagalan, meskipun teknik telah dijelaskan untuk meningkatkan visualisasi permukaan kegagalan (misalnya Griffiths & Kidger, 1995).

Metode FE yang lebih maju untuk pemodelan pita geser dalam hubungannya dengan teknik perbaikan mesh adaptif telah dijelaskan oleh Loret & Prevost (1991) dan Zienkiewicz et al. (1995).

Slope stability analysis by finite elements by D. V. Griffiths Colorado School of Mines at Grif®ths, D. V. & Lane, P. A. (1999). GeÂotechnique 49, No. 3, 387±403

Read More

Limit Equilibrium Method (LEM) atau Metode Kesetimbangan Batas

Metode limit equilibrium atau metode kesetimbangan batas adalah salah satu metode yang paling umum digunakan untuk menganalisa permasalahan kestabilan dinding lereng. Berbagai metode juga telah dikembangkan oleh banyak peneliti untuk menghitung nilai dari faktor keamanan selama bertahun tahun. 

Rumus perhitungan The General Limit Equilibrium (GLE) atau metode kesetimbangan batas yang dikembangkan pada tahun 1970 oleh Fredlund. Rumus ini mencakup dua persamaan faktor keamanan berdasarkan dari rumus GLE dan memiliki beberapa asumsi mengenai gaya normal pada bidang perlapisan batuan. Perhitungan GLE memberikan nilai Faktor Keamanan berdasarkan dari perhitungan kesetimbangan momen (Fm) dan kesetimbangan gaya horizontal (Ff). 

Morgenstern and Price (1965) mengusulkan suatu persamaan yang dapat menangani gaya geser antar perlapisan dalam GLE dan hal tersebut memenuhi kesetimbangan antara momen dan gaya. Dalam menghitung besar faktor keamanan lereng dalam analisis lereng tanah melalui metoda sayatan, hanya longsoran yang mempunyai bidang gelincir yang dapat dihitung.

Longsoran dengan bidang gelincir (slip Surface), F dapat dihitung dengan metode sayatan (slice method) menurut Fellinius atau Bishop. Untuk suatu lereng dengan penampang yang sama, cara Fellinius dapat dibandingkan nilai faktor keamanannya dengan cara Bishop.

LEM adalah metode yang menggunakan prinsip kesetimbangan gaya. Metoda analisis ini pertama-tama mengasumsikan bidang kelongsoran yang dapat terjadi. Terdapat dua asumsi bidang kelongsoran yaitu: bidang kelongsoran berbentuk circular dan bidang kelongsoran yang diasumsikan berbentuk non-circular (bisa juga planar).

Gambar 1 - Bidang Longsor Circular 

Gambar 2- Bidang Longsor Non-Circular 

Gambar 3 Gaya yang bekerja pada bidang irisan

Perhitungan dilakukan dengan membagibagi tanah yang berada dalam bidang longsor dalam irisan-irisan sebagaimana diperlihatkan dalam Gambar 1 hingga Gambar 3, karena itu metoda ini dikenal juga dengan nama metoda irisan (method of slice). Gambar 3 yang menggambarkan massa tanah dan gaya-gaya yang bekerja pada irisan.

Berbagai solusi yang berbeda untuk metode irisan ini telah dikembangkan selama bertahun-tahun, dimulai dari Fellenius, Taylor, Bishop, Morgenstern-Price, Janbu hingga Sarma dan lainnya. Perbedaan antara cara yang satu dengan yang lain tergantung pada persamaan kesetimbangan batas dan asumsi gaya kekuatan antar irisan (interslice force) yang diperhitungkan.

Fellenius merupakan orang pertama yang mempublikasikan metoda irisan ini dan merupakan cara yang paling sederhana. Pada cara Fellenius semua gaya antar irisan diabaikan dan hanya memperhitungkan kesetimbangan momen. Bishop kemudian mengembangkan cara yang lebih kompleks dengan memasukkan gaya yang bekerja di sekitar bidang irisan, namun tetap melakukan perhitungan dengan kesetimbangan momen. Bishop juga mengeluarkan cara yang dikenal dengan nama Metode Bishop Sederhana (Simplified Bishop Method) dimana gaya normal antar irisan diperhitungkan tetapi gaya geser antar irisan diabaikan. Janbu mengembangkan metoda yang mirip dengan metoda sederhana Bishop. Perbedaannya adalah metoda Janbu diturunkan dari kesetimbangan gaya horisontal.

Tabel 1 dan 2 menunjukkan perbedaan antar metoda yang dikenal dalam LEM. 

Tabel 1 Kesetimbangan yang Diperhitungkan pada masing-masing metode

Tabel 2 Gaya Antar Irisan yang Bekerja masing - masing metode.

Dalam LEM ini faktor keamanan, SF, ada prinsipnya dihitung dari perbandingan antara kuat geser tanah, 𝛕f, dengan gaya dorong,𝛕, atau perbandingan antara momen tahan, RM, terhadap momen dorong, DM, sebagaimana ditunjukkan dalam persamaan (1) di bawah ini:

Source ; ANALISA STABILITAS LERENG  LIMIT EQUILIBRIUM vs FINITE ELEMENT METHOD oleh Ir. GOUW Tjie Liong, M.Eng, ChFC, Fakultas Teknik Sipil, Universitas Bina Nusantara & Dave Juven George Herman, Fakultas Teknik Sipil, Universitas Bina Nusantara Pada HATTI‐PIT‐XVI 2012, 4‐5 Dec 2012, Hotel Borobudur, Jakarta.

Read More

Teori Mohr Coloumb

Di beberapa artikel sebelumnya kita sering menyinggung tentang Teori Mohr Coloumb, kali ini saya akan mencoba menjelaskan apa sebenarnya teori tersebut, silahkan disimak ya.

Mohr menjelaskan bahwa keruntuhan sebagai akibat dari kombinasi kritis antara tegangan normal dan geser dan bukan hanya akibat tegangan normal maksimum dan tegangan geser maksimum saja. Sehingga pada bidang keruntuhan dapat dinyatakan bahwa :  

Tapi sebelum kita membahas lebih lanjut ada baiknya kita coba pahami dulu teori terkait tegangan (σ)  dan regangan (ε).

Tegangan (σ)

Jika sebuah benda elastis ditarik oleh sebuah gaya, benda tersebut akan bertambah panjang sampai ukuran tertentu. Besarnya tegangan (stress) adalah perbandingan antara gaya tarik yang bekerja terhadap luas penampang benda. Tegangan dinotasikan dengan σ (sigma), satuannya Nm-2. Secara matematis, tegangan dirumuskan dengan:

σ = F(N)/A(m2)

Tegangan menunjukkan kekuatan gaya yang menyebabkan benda berubah bentuk.

Misalnya, jika ada dua buah batuan yang sama tetapi dengan luas penampang berbeda dan diberi gaya, kedua batuan tersebut akan mengalami tegangan yang berbeda. batuan dengan luas penampang yang lebih kecil akan mengalami tegangan yang lebih besar daripada batuan dengan luas penampang yang lebih besar. 

Regangan (ε)

Regangan ialah perubahan relatif ukuran atau bentuk benda yang mengalami tegangan. Gambar diatas memperlihatkan sebuah batang yang mengalami regangan akibat gaya tarik F. Panjang batang mula-mula adalah Lo. Setelah mendapat gaya tarik sebesar F, batang tersebut berubah panjangnya menjadi L. dengan demikian, batang tersebut mendapatkan pertambahan panjang sebesar , dengan persamaan 

∆L= L-Lo .

Oleh karena itu, regangan didefinisikan sebagai perbandingan antara pertambahan panjang benda dan panjang benda mula-mula. Secara matematis dirumuskan:

Regangan (ε) = ∆L/Lo

Apabila tegangan (stress) digambarkan pada suatu diagram, maka akan diperoleh kurva yang bentuknya berbeda-beda yang sesuai dengan material yang diuji tegangannya. Gambar dibawah menunjukkan bentuk umum kurva tegangan dari suatu benda.

Kurva itu menunjukkan pertambahan panjang suatu benda atau bahan terhadap gaya yang diberikan padanya. Sampai suatu titik yang disebut batas proporsional. Kemudian pada satu titik tertentu benda itu sampai pada batas elastik dimana benda itu akan kembali ke panjang semula jika gaya dilepaskan. Jika benda diregangkan melewati batas elastik, maka akan memasuki daerah plastis dimana benda tidak akan kembali ke panjang awalnya ketiga gaya eksternal dilepaskan, tetapi tetap berubah bentuk secara permanen (seperti melengkungnya sebatang besi). Perpanjangan maksimum dicapai pada titik patah (titik pulus). Gaya maksimum yang dapat diberikan tanpa benda itu patah disebut sebagai kekuatan maksimum dari materi/benda itu.

Oke kembali pada teori Mohr-Coloumb ya.

Kriteria Failure Mohr Coloumb adalah sauatu rangkaian persamaan linear dalam pada tegangan utama yang menggambarkan kondisi-kondisi di mana material isotropik akan Failure, dengan mengabaikan efek dari  tegangan menengah (σ2).

Mohr Coloumb dapat ditulis sebagai fungsi dari;

(1) tegangan utama (σ1) dan tegangan minor (σ3) dan atau 

(2) tegangan normal (σ) dan tegangan geser (𝜏) pada bidang failure (Jaeger and Cook 1979). .

Ketika seluruh tegangan utama (major stress) adalah gaya tekan, percobaan menunjukkan bahwa kriteria berlaku cukup baik untuk batuan, di mana nilai kuat tekan uniaksial (UCS)  jauh lebih besar dari dari nilai  kuat tarik uniaksial (T). 

Beberapa modifikasi dibutuhkan ketika ada potensi dari tegangan tarik, karena kekuatan tarik (teoritis) uniaksial (T) yang diprediksi dari MC tidak diukur dalam percobaan. 

Kriteria MC dapat dianggap sebagai kontribusi dari Mohr dan Coulomb (Nadai 1950).

Kondisi Mohr didasarkan pada asumsi bahwa Failure hanya bergantung pada tegangan utama (σ1) dan tegangan minor (σ3), dan bentuk dari failure envelope, dan (σ), (𝜏) yang bekerja pada bidang Failure, dapat berupa rergresi linier atau nonlinier (Mohr 1900).  

Kondisi Coulomb didasarkan pada failure envelope linier untuk menentukan kombinasi kritis (σ), (𝜏) yang akan menyebabkan failure pada beberapa bidang (Coulomb 1776). 

Kriteria keruntuhan Mohr-Coulomb ditunjukan oleh garis lurus yang di kenal dengan Mohr-Coulomb failure envelope. Garis ini menunjukan batas kondisi stabil dari keruntuhan. Regangan yang berada di bawah garis adalah keadaan stabil. Sedangkan keruntuhan terjadi ketika teganga menyentuh atau melewati garis keruntuhan Mohr-Coulomb.

Pada kriteria Mohr-Coulomb selubung keruntuhan dianggap srbagai garis lurus untuk mempermudah perhitungan. Kriteria ini didefinisikan sebagai berikut :

Dimana : τf = tegangan Geser maksimum; c = Kohesi; 𝜎𝑛 =Tegangan Normal Pada Bidang Tinjauan; Tan φ = Koefisien Gesek antar Partikel; φ = Sudut geser Dalam.

lebih jeasnya τf adalah tegangan geser maksimum yang dapat diambil tanah sebelum Failure, di bawah tegangan normal σ.

Untuk tanah jenuh air , tegangan normal total pada titik tersebut adalah penjumlahan dari tegangan efektif (𝜎’) dan tekanan air pori (u).

Pada ilustrasi dibawah ini sampel batuan/tanah tidak mengalami failure/ keruntuhan karena selubung mohr berada dibawah failure envelope.

Seiring dengan bertambahnya tegangan normal (σ), selubung mohr bertambah besar dan menyentuh  mohr failure envelope, maka terjadilah keruntuhan pada sampel tersebut.

Seperti yang sudah kita bahas pada beberapa judul artikel sebelumnya teori Mohr-Coloumb ini kita gunakan pada beberapa pengujian lab seperti direct shear test dan triaxial test. silahkan dibaca disini ya;

Triaxial Test

Direct Shear Test

Kita cukupkan dulu pembahasannya ya tentang teori Mohr Coloumb, jika ada yang kurang jelas dan ingin ditanyakan dapat langsung di kolom komentar.

Semoga Bermanfaat

Sumber;

https://www.researchgate.net/publication/257445185_Mohr-Coulomb_Failure_Criterion

https://nptel.ac.in/courses/105101001/downloads/L54.pdf

http://www.ocw.upj.ac.id/files/Slide-TSP204-PERTEMUAN-13-14-KRITERIA-KERUNTUHAN-MOHR-COULOMB.pdf

https://eandroidfisika.wordpress.com/tegangan-regangan-dan-modulus-elastisitas/

https://fisikazone.com/tegangan-stress/

https://www.toppr.com/guides/physics/mechanical-properties-of-solids/hookes-law-and-stress-strain-curve/

Read More

Pengujian Triaksial atau Triaxial Test

Sebelum kita bahas lebih rinci tentang triaksial test untuk mendapatkan parameter mekanika tanah atau batuan seperti kohesi (C) dan sudut geser dalam (Φ), ada baiknya dipahami bahwa terdapat perbedaan tipe pengujian triaksial test dan hubungannya dengan pengujian pada sampel batuan dan pada sampel tanah, karena pengujian triaksial di dunia teknik sipil dan dunia teknik pertambangan agak berbeda, penjelasan lebih lanjut dapat dilihat pada bagian akhir,

Secara sederhana yang membedakan anatara triksial dan direct shear test adalah; pada direct shear test diberikan gaya normal konstan pada bidang vertical (Fz) dan kemudian diberikan gaya geser pada bidang horizontal (Fx) sampai batuan pecah atau mengalami keruntuhan, sedangkan pada pengujian triaksial diberikan gaya tekan konstan diseluruh arah pada bidang lateral/ horizontal sampel batuan (σ3) dan kemudian diberikan gaya tekan pada bidang aksial / vertical atau (σ1) hingga batuan mengalami keruntuhan.

Gamba1. (Atas) Triaxial Test dan (Bawah) Direct Shear Test.

Pada tes kompresi triaksial konvensional, suatu spesimen silinder yang dibungkus dengan membran karet dan diletakkan pada suatu sel triaksial di mana dia dikenakan tekanan fluida. Suatu beban kemudian diberikan mengikuti sumbu spesimen, menaikan tegangan sumbu sampai keruntuhan terjadi. Pada kondisi-kondisi tersebut, tegangan-tegangan minor dan pertengahan, masing masing σ3 dan σ2, sama dengan tekanan fluida; tegangan utama mayor, σ1, disediakan oleh baik tekanan fluida dan tegangan aksial yang diberikan oleh piston beban. Tegangan deviator atau perbedaan tegangan utama adalah (σ1- σ3) yaitu perbedaan antara tegangan-tegangan utama mayor dan minor.

Kondisi-kondisi drainase selama pemberian tekanan sel dan beban aksial, masing-masing menjadi dasar klasifiksasi umum tes kompresi triaksial ada 3 yaitu;

• Tak terkonsolidasi dan tak terdrainase (UU). Pada tes ini, suatu tekanan sel diberikan pada spesimen tes dan tegangan deviator atau penggeseran diberikan segera setelah tekanan sel stabil. Drainase tidak diizinkan selama pemberian tekanan sel (tegangan keliling) dan drainase tidak diizinkan selama pemberian tegangan deviator. Pengujian Unconsolidated Undrained (UU) dilakukan untuk mensimulasikan kondisi di lapangan apabila penambahan/pemberian beban relatif cepat sehingga lapisan tanah belum sempat terkonsolidasi (air di dalam pori tanah tidak sempat mengalir ke luar selama proses pemberian beban), oleh karena itu pengujian ini juga dinamakan quick test. Sebagai contoh dalam kasus ini adalah suatu lapisan tanah yang menerima beban relatif cepat seperti beban urugan yang berlangsung relatif singkat.

• Terkonsolidasi-tak terdrainase (CU). Pada tes ini, drainase diizinkan selama pemberian tegangan keliling dan spesimen sepenuhnyan terkonsolidasi di bawah tegangan ini. Drainase tidak diizinkan selama pemberian tegangan deviator. Pengujian Consolidated Undrained (CU) dilakukan untuk mensimulasikan kondisi lapisan tanah yang telah terkonsolidasi dan kemudian menerima penambahan beban yang relatif cepat. Pada kasus ini mula-mula air di dalam pori tanah dibiarkan mengalir keluar akibat proses konsolidasi, dan setelah tanah terkonsolidasi sempurna (100%), lapisan tanah tersebut menerima tambahan beban yang relatif cepat sehingga air di dalam pori tanah pada saat penambahan beban tidak sempat mengalir ke luar. Sebagai contoh pada kasus ini adalah beban tanki yang didirikan di atas suatu urugan pada tanah lempung yang telah mengalami konsolidasi 100%.

• Terkonsolidasi-terdrainase (CD). Pada tes ini, drainase diizinkan baik selama pemberian tegangan keliling dan tegangan deviator sehingga spesimen sepenuhnya terkonsolidasi di bawah tegangan keliling dan tekanan pori ekses tidak terbentuk selama penggeseran. Pengujian Consolidated Drained (CD) dilakukan untuk mensimulasikan kondisi pemberian beban pada tanah yang telah terkonsolidasi dengan kecepatan yang relatif lambat dibandingkan dengan keluarnya air dari pori tanah.

Kita bahas lebih rinci mengenai ketiga tipe pengujian ini;
--------------------------------------------------------------------------------------------------------------------------

1. Tes Tak Terkonsolidasi-Tak Terdrainase (UU)


ASTM D2850-87 menjelaskan suatu metode standar untuk menentukan kuat tekan tak terkonsolidasi, tak terdrainase tanah kohesif pada kompresi triaksial.

Hal-hal berikut berkenaan dengan metode tes dibuat:

• Suatu prosedur untuk mendapatkan pengukuran tekanan pori tidak dimasukkan.
• Keruntuhan didefinisikan sebagai tegangan pada spesimen berkaitan dengan tegangan deviator maksimum yang dicapai atau tegangan deviator pada regangan aksial 15%, tergantung yang mana tercapai terlebih dahulu selama pengetesan.
• Jika spesimen tes sepenuhnya jenuh, selubung keruntuhan Mohr biasanya akan berupa garis lurus horizontal sepanjang keseluruhan tegangan keliling yang bekerja pada spesimen; pada kasus tanah-tanah yang jenuh sebagian, selubung keruntuhan Mohr failure biasanya melengkung
• Beban diberikan sedemikian rupa sehingga menghasilkan regangan aksial pada suatu laju sekitar 1% per menit untuk bahan-bahan plastik, dan 0,3% per menit untuk bahan-bahan getas yang mencapai tegangan deviator maksimum pada sekitar 3 sampai 6 % regangan. Pembebanan dilanjutkan sampai mencapai 15% regangan aksial tetapi bisa dihentikan jika tegangan deviator telah mencapai puncak dan kemudian turun 20%, atau regangan aksial telah mencapai 5% di luar regangan di mana tegangan deviator puncak terjadi.
• Beban yang cukup dan pembacaan deformasi harus diambil untuk mendefinisikan kurva tegangan-regangan.
• Suatu sketsa atau foto harus dibuat berisi spesimen tes pada saat keruntuhan, memperlihatkan sudut kemiringan bidang keruntuhan jika sudut terlihat dan dapat diukur.

Suatu selubung keruntuhan Mohr yang tidak horizontal pada suatu lempung lunak kemungkinan pertanda bahwa sampel tidak sepenuhnya jenuh. Hal ini harus disebutkan pada lembar pengujian dan jika suatu nilai f didapati hasil tersebut harus disertai dengan suatu catatan berisi peringatan.

Gambar 2. Ilustrasi Pengujian Triaksial Unconsolidated undrained.

Penerapan;

Kekuatan triaksial yang didapat pada kondisi-kondisi tak terkonsolidasi tak terdrainase berlaku untuk situasi-situasi desain di mana pembebanan sangat cepat sehingga tidak cukup waktu untuk tekanan air pori yang terbentuk untuk berdisipasi dan untuk konsolidasi terjadi (artinya drainase tidak terjadi). Kekuatan triaksial yang diukur pada kondisi-kondisi UU digunakan untuk menentukan kekuatan pada akhir konstruksi. Konstruksi timbunan pada deposit lempung merupakan suatu contoh situasi di mana kuat geser tak terdrainase in situ akan menentukan stabilitas.

Perlu dicatat bahwa kuat geser tak terdrainase ôf, tegangan geser pada bidang keruntuhan pada saat keruntuhan diambil sebagai setengah kuat tekan tak terdrainase (σ1-σ3 ) yaitu;

σf = (σ1 - σ3)/2

--------------------------------------------------------------------------------------------------------------------------

2. Tes Terkonsolidasi-Tak Terdrainase (CU)

Suatu metode standar untuk melaksanakan tes kompresi triaksial terkonsolidasi tak terdrainase pada tanah-tanah kohesif dijelaskan pada ASTM D4767-88.

Hal hal berikut dibuat berkenaan dengan penjelasan metode tes:

• Spesimen yang dikonsolidasikan secara isotropis digeser tak terdrainase pada kompresi dengan laju deformasi aksial yang konstan (kontrol regangan).
• Metode tersebut menyediakan perhitungan tegangan total dan efektif pada, dan kompresi aksial spesimen tes melalui pengukuran beban aksial, deformasi aksial dan tekanan air pori.
• Kekuatan dan sifat-sifat deformasi tanah-tanah kohesif, seperti selubung kekuatan Mohr dan modulus Young, bisa ditentukan dari data tes.
• Tiga spesimen biasanya diuji pada tegangan konsolidasi efektif yang berbeda untuk membuat suatu selubung kekuatan.
• Keruntuhan sering diambil berkaitan dengan tegangan deviator maksimum yang dicapai atau tegangan deviator yang dicapai pada 15% regangan aksial, tergantung yang mana dulu tercapai pada tes. Bergantung pada perilaku tanah dan aplikasi lapangan, kriteria keruntuhan lainnya bisa didefinisikan seperti rasio tegangan utama efektif σ'1/σ'3, atau tegangan deviator pada regangan aksial yang dipilih selain 15%.
• Tekanan air pori bisa diukur menggunakan kalau tidak transducer tekanan elektronik yang sangat kaku atau suatu alat yang menandakan nol.
• Komponen-komponen konsolidasi dan penggeseran dari tes harus dilakukan pada suatu lingkungan di mana fluktuasi suhu kurang dari ±4°C dan tidak ada kontak langsung dengan cahaya matahari.
• Penjenuhan dicapai dengan memberikan tekanan balik pada air pori spesimen untuk membuat udara pada rongga pori menjadi larutan pada air pori. Derajat penjenuhan diukur menggunakan parameter tekanan pori B yang didefinisikan sebagai: B = (Äu/Äs3 ) di mana: Äu = perubahan tekanan pori spesimen yang terjadi sebagai akibat perubahan tekanan sel pada saat katup drainase spesimen tertutup dan Äs3 = perubahan tekanan sel.
• Selama konsolidasi, data-data didapat untuk penggunaan pada penentuan kapan konsolidasi selesai dan untuk menghitung laju regangan yang akan digunakan untuk komponen penggeseran tes.
• Konsolidasi dibiarkan berlanjut selama sekurang-kurangnya satu seri log waktu atau satu periode semalam setelah 100% konsolidasi primer dicapai, seperti yang ditentukan oleh salah satu prosedur yang dijelaskan di ASTM D2435-90; waktu untuk 50% konsolidasi primer, t50, ditentukan oleh salah satu prosedur yang dijelaskan di ASTM D2435-90.
• Jika keruntuhan diasumsikan terjadi setelah 4% regangan aksial, laju regangan yang sesuai bisa diperoleh dengan membagi 4% terhadap 10 kali nilai t50; jika diperkirakan keruntuhan akan terjadi pada nilai regangan yang lebih rendah dari 4%, laju regangan yang sesuai didapat dengan membagi regangan pada saat keruntuhan dengan 10 kali nilai t50.
• Suatu sketsa atau foto harus dibuat mengenai spesimen yang runtuh yang memperlihatkan cara keruntuhan (bidang geser, penonjolan, dan sebagainya).

Gambar 3. Ilustrasi Pengujian Triaksial Consolidated Undrained.

Penerapan;

Kuat geser pada tes ini diukur pada kondisi-kondisi tak terdrainase dan bisa diterapkan untuk kondisi lapangan di mana; (i) tanah-tanah yang telah sepenuhnya dikonsolidasikan pada satu rangkaian tegangan diberi suatu perubahan tegangan tanpa kesempatan konsolidasi lebih lanjut terjadi dan (ii)

kondisi-kondisi tegangan lapangan mirip dengan yang di tes.

Karena pengukuran tekanan air pori dilakukan, kuat geser bisa dinyatakan dalam bentuk tegangan efektif dan bisa diterapkan untuk kondisi-kondisi lapangan di mana (i) drainase sempurna bisa terjadi atau (ii) di mana tekanan pori yang timbul akibat pembebanan bisa diperkirakan dan (iii) di mana kondisi-kondisi tegangan lapangan mirip dengan yang di lapangan. Kuat geser yang didapat dari tes, dinyatakan dalam bentuk tegangan-tegangan total atau efektif, biasanya digunakan pada analisis stabilitas timbunan.

--------------------------------------------------------------------------------------------------------------------------

3. Tes Terkonsolidasi-Terdrainase (CD)

Tahap-tahap penjenuhan, konsolidasi dan kompresi dari sebuah tes kompresi triaksial terkonsolidasi terdrainase dengan pengukuran perubahan volume dijelaskan pada Klausa 5,6 dan 8, masing-masing pada BS 1377: Part 8 : 1990. Untuk kemudahan perujukan, klausa-klausa tersebut dicantumkan di sini pada Appendiks B. Persiapan contoh tak terganggu untuk pengujian dijelaskan pada

Appendiks C.

Tahap Penjenuhan

Dua prosedur penjenuhan dijelaskan:

• Penjenuhan dengan memberikan kenaikan tekanan sel dan tekanan balik secara bergantian. Tahap-tahap kenaikan tekanan sel dilaksanakan tanpa membiarkan drainase masuk atau keluar spesimen, yang memungkinkan nilai-nilai koefisien tekanan pori B untuk ditentukan pada masing-masing tingkatan tekanan total
• Penjenuhan dengan hanya menaikkan tekanan sel; air tidak diizinkan untuk masuk atau keluar spesimen selama prosedur ini sehingga diberi nama "penjenuhan pada kadar air yang konstan".

Pada prosedur pertama spesimen dianggap jenuh jika tekanan pori tetap stabil setelah 12 jam, atau semalam, dan nilai B sama dengan atau lebih besar dari 0,95. Pada prosedur kedua, spesimen dianggap jenuh jika salah satu kriteria ini dipenuhi.

Tahap Konsolidasi

Tahap konsolidasi berlangsung segera setelah tahap penjenuhan dan memakai alat yang sama. Tujuan dari tahap ini adalah untuk membuat spesimen berada dalam keadaan tegangan efektif yang dibutuhkan untuk melaksanakan tes kompresi.

Data dari tahap konsolidasi digunakan untuk:

• Memperkirakan laju regangan yang cocok untuk diterapkan selama tes kompresi
• Menentukan kapan konsolidasi selesai
• Menghitung dimensi spesimen pada permulaan tahap kompresi.

Konsolidasi spesimen dilanjutkan sampai tidak ada lagi perubahan volume yang signifikan dan sampai derajat konsolidasi U, seperti didefinisikan dalam prosedur, sama dengan atau lebih besar dari 95%.

Suatu grafik perubahan volume yang terukur terhadap akar kuadrat waktu diplot dan suatu metode penentuan t100 dari grafik dijelaskan; t100 digunakan untuk memperkirakan waktu pengujian yang siginifikan (dalam menit) pada tes kompresi dan sebab itu laju perpindahan aksial.

Formula-formula disajikan untuk menghitung koefisien konsolidasi cv (m²/tahun), dan koefisien kompresibilitas volume mv (m²/MN) untuk konsolidasi isotropik. Faktor-faktor yang akan digunakan waktu menghitung cv, dan waktu pengujian yang signifikan pada tes kompresi, diberikan pada sebuah

tabel sebagai fungsi kondisi drainase selama konsolidasi.

Tahap Kompresi

Selama kompresi, drainase bebas air pori dari spesimen diizinkan. Volume cairan pori yang keluar atau masuk spesimen diukur melalui indikator perubahan volume pada garis tekanan balik dan sama dengan perubahan volume spesimen selama geser; tekanan pori bisa dimonitor pada dasar alat sebagai suatu pengetesan efisiensi drainase.

Tes dilaksanakan dengan cukup lamban untuk menjaga perubahan-perubahan tekanan pori akibat penggeseran dapat diabaikan. Kompresi diberi pada suatu laju perpindahan aksial (dr, dalam mm/min) sedekat mungkin terhadap, tetapi tidak melebihi yang diberikan oleh formula:

dr = (åf ×Lc)/tf

di mana;

• Lc = panjang spesimen yang terkonsolidasi, mm
• åf = interval regangan yang signifikan untuk spesimen tes
• tf = waktu pengujian yang siginifikan, menit

Nilai tf diberikan sebagai:

• tf = Ft100

di mana F diambil dari tabel yang disebutkan sebelumnya. Sebagai contoh, jika rasio tinggi terhadap diameter spesimen adalah 2 dan drainase selama konsolidasi adalah dari batas radial dan kedua ujung,

nilai F untuk suatu tes terdrainase adalah 16.

Nilai åf diperkirakan dengan mempertimbangkan hal-hal berikut:

1. Jika hanya kondisi tegangan pada saat keruntuhan (seperti didefinisikan di bawah) yang signifikan, åf adalah regangan perkiraan pada saat keruntuhan akan terjadi.
2. Jika pembacaan-pembacaan antara yang memiliki rentang kurang lebih sama, masing-masing membutuhkan penyamaan tekanan pori, adalah signifikan, åf adalah kenaikan regangan antara masing-masing pembacaan.

Kriteria untuk kondisi tegangan pada saat keruntuhan diberikan pada Klausa 1 BS 1377 : Part 8 : 1990 dan adalah sebagai berikut:

• Tegangan maksimum deviator, yaitu perbedaan tegangan utama maksimum, (σ1-σ3)f.
• Rasio tegangan utama efektif maksimum, σ'1/σ '3.
• Jika penggeseran berlanjut pada tekanan pori yang konstan (kondisi tak terdrainase) atau tanpa perubahan volume (kondisi terdrainase), di kedua kasus pada tegangan geser yang konstan.

Tekanan pori harus diamati secara periodik dan jika dia bervariasi terhadap nilai-nilai tekanan balik dengan lebih dari 4% tekanan keliling efektif, laju regangan harus dikurangi 50% atau lebih.

Sekurangnya 20 rangkaian pembacaan pengukur deformasi, alat gaya dan pengukur perubahan volume harus dilakukan agar kurva tegangan-regangan dapat didefinisikan secara jelas di sekitar keruntuhan. 

Tes dilanjutkan sampai kondisi-kondisi berikut telah secara jelas diidentifikasi:

• Tegangan deviator maksimum, atau;
• Deformasi geser tetap berlangsung pada volume konstan dan tegangan geser konstan.

Jika tidak satupun kondisi-kondisi keruntuhan yang diperlukan nampak, tes dihentikan pada regangan aksial 20%; pada kasus ini kuat geser tidak dilaporkan.

Gambar 4. Ilustrasi Pengujian Triaksial Consolidated Drained.

Penerapan

Hasil-hasil tes CD yang dilakukan pada tanah kohesif bisa diterapkan pada situasi-situasi di mana konstruksi akan berlangsung pada laju yang cukup lambat sehingga tidak ada tekanan pori ekses yang terjadi atau waktu yang cukup telah lewat sehingga semua tekanan pori ekses telah terdisipasi (AASHTO 1988).

--------------------------------------------------------------------------------------------------------------------------

Penjelasan diatas kalau dicermati dengan baik hanya membahas pengujian untuk sampel tanah dalam kondisi pekerjaan sipil, sedangkan untuk kita yang bekerja pada bidang pertambangan tentu tidak hanya berhubungan dengan tanah saja tetapi juga berhubungan dengan batuan, maka dalam hal ini kita harus memahami dua mekanika yang serupa tapi tak sama yaitu mekanika tanah dan mekanika batuan.

Sekarang mari kita bahas, pada dasarnya ketiga jenis test ini tergantung pada proses konsolidasi dan tegangan air pori (pore water perssure) dan hubungannya ke proses drainasi pada tanah, yang jadi pertanyaan adalah apa proses konsolidasi juga terjadi pada batuan ? kalau tegangan air pori tentu ada tergantung dari permeabilitas dan porositas batuannya seperti yang telah kita bahas disini. 

Untuk mengerti pertanyaan tersebut mari coba kita pahami arti dari proses konsolidasi tanah;

Konsolidasi adalah proses pemampatan tanah akibat adanya beban tetap dalam jangka waktu tertentu. Pemampatan awal pada umumnya adalah disebabkan oleh pembebanan awal (preloading). Konsolidasi Primer yaitu periode selama tekanan air pori secara lambat laun dipindahkan ke dalam tegangan efektif, sebagai akibat dari keluarnya air dari pori-pori tanah. Konsolidasi sekunder terjadi setelah tekanan air pori hilang seluruhya. Pemampatan yang terjadi di sini disebabkan oleh penyesuaian yang bersifat plastis dari butir-butir tanah.

Berarti dari pengertian diatas proses konsolidasi tidak terjadi pada batuan massive atau batuan yang relatif kompak sehingga pada sampel batuan dilakukan pengujian minimal 5 sampel dengan pemberian gaya dengan nilai σ3 yang berbeda beda kemudian ditekan pada bidang vertical atau diberikan tegangan aksial (σ1) hingga batuan mengalami keruntuhan. Pada uji ini, tegangan menengah dianggap sama dengan nilai tekanan pemampatan  σ2 = σ3.

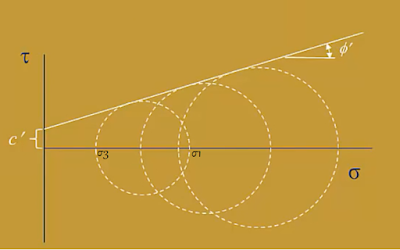
Nilai dari σ3 dan σ1 dari 5 sampel tersebut kemudian dapat diplot pada dengan menggunakan selubung mohr coloumb, dan tentukan garis regressi sehingga didapat nilai Kohesi dan sudut geser dalamnya.

Gambar 5. Ilustrasi Selubung Mohr Coloumb.

Kemudian dari pengalaman pribadi ketika melakukan pengujian triaxial di laboratorium mekanika batuan ITB fluida yang digunakan pada saat pengujian adalah oli sedangkan seperti kita ketahui bersama secara umum pengujian triaksial dilakukan dengan menggunakan fluida air. Hal ini mungkin berkaitan viskositas fluida dan gaya tekan yang bekerja terhadap sampel batuan, CMIIW.

Gambar 6. Mesin/ Alat Uji Triaksial di Lab ITB.

Gambar 7. Software pengukur kekuatan tekan aksial (σ1).

Gambar 8. Batuan mengalami keruntuhan pada saat diberikan tekanan aksial maksimum (σ1).

Karena tulisan ini sudah terlalu panjang, maka kita cukupkan sampai disini dulu, jika ada yang meragukan atau kurang jelas kita bisa diskusikan di kolom komentar atau langsung email ke saya, insyallah saya bales, hehe;

Semoga Bermanfaat, see ya

Credits and Thanks to;

• Buku Panduan Geoteknik oleh Pusat Litbang Prasarana Transportasi, Bandung melalui Kontrak Proyek Tahap 2, Indonesian Geotechnical Materials and Construction Guides. Edisi Pertama Nopember 2001.
• Buku Geoteknik Tambang, Irwandi Arif, 2016
• Buku Mekanika Batuan, Made Astawa Rai, S Karmadibrata, R.K. Wattimena
• https://james-oetomo.com/2013/07/26/uji-triaksial-geser-kilasan-umum/
• http://warungsipil.blogspot.com/2017/02/konsolidasi-tanah.html
• https://andrieasgunawan.blogspot.com/2013/03/mekanika-tanah-2-konsolidasi-dan.html
• Ilustrasi Gambar dari video youtube ini

Read More